Decades of research has shown that we’re not very sensitive to distortion at bass frequencies. I doubt if anything has happened to our species recently that would change that. Consider the science settled. The problem with scientific findings is, it’s frightfully easy to miss the fine print and draw the wrong conclusions.
I’d like to propose a simple demo to illustrate this. I’ve simulated two highly simplified woofers, both of which are ideal except that one has a nonlinear Kms (but a perfectly constant BL=1) and the other a nonlinear BL but a perfectly linear suspension (Kms=1). Never mind the units, it’s a simulation so I normalized as many of the values to 1 as I sensibly could.
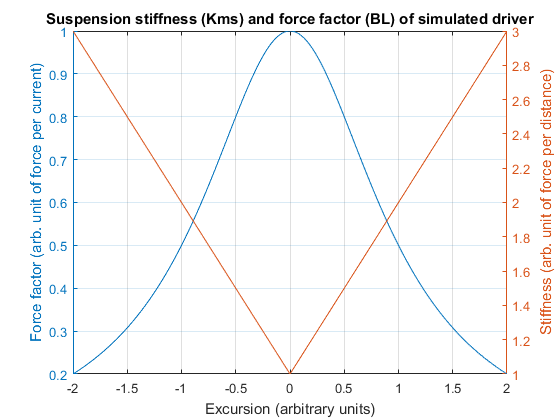
Stiffness and Q are set for a 40Hz Butterworth roll-off. As you can see from the graph I’m not trying to make this demo at all subtle. After all, most of you will be using PC speakers or earbuds at best to listen to the sound samples.
The magnitude and nature of the two nonlinearities was chosen such that the resulting harmonic distortion is about equally bad in either case:
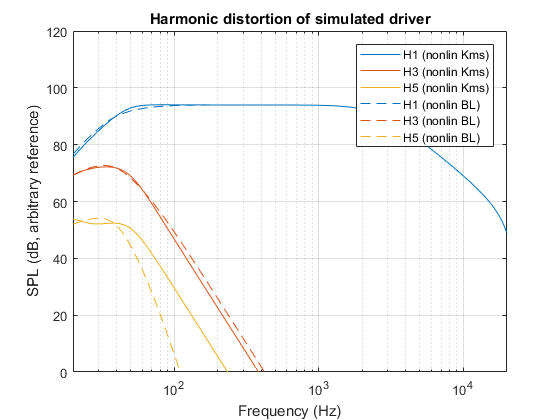
The armchair psychoacoustician will conclude that any audible differences between these two drivers are going to be very subtle indeed.
Let’s run some audio through them and listen to the result. For good order I’ve inserted a 2.5kHz low pass filter to make the sound samples representative of midwoofer use. I’ve also included a third one where both Kms and BL are set to a constant value of 1 so you have a distortion free reference to listen to as well.
Driver with only nonideal suspension stiffness Kms:
Driver with only nonideal force factor BL:
Fully distortion free driver:
I hope you’re duly startled. Just to show that I’m not cheating, here’s a plot of the cone position of both simulated drivers, between seconds 6 and 8 of the clip.

It’s basically the same cone movement. Give or take. The bass distortion is also fairly similar, and very large. What happens though is that the “give or take” includes midrange content which doesn’t move the cone noticeably, but which is clearly much more affected when the force factor changes compared to when stiffness changes. The reason is that only low frequency forces are working to overcome the suspension. From the resonance frequency upward, the cone mass is a much greater drag on the voice coil than the suspension. Transducer designers say that at high frequencies “the system is mass controlled” (further expanded on in another blog post about moving mass, “speed” and bandwidth). So, if Kms is the only cause of low frequency distortion, it will not cause distortion at higher frequencies. If BL is a cause of low frequency distortion, it will also amplitude modulate higher frequency components (i.e. produce IMD, intermodulation distortion). We don’t so much hear distortion levels as distortion mechanisms. You need to understand the mechanism before you can design a test that will quantify it sensibly.
Fortunately it’s not all that complicated here. Just apply a low-frequency sine wave and a mid-frequency sine wave together and look at the spectrum that comes out in either case:
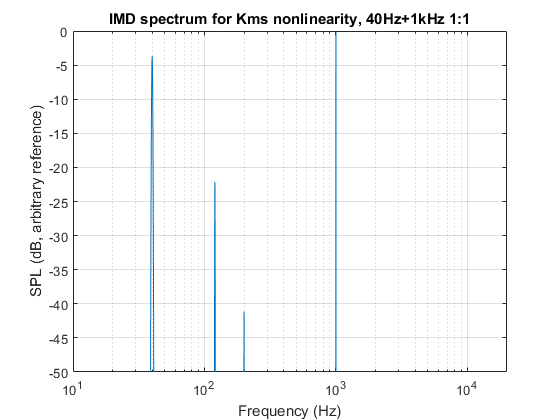
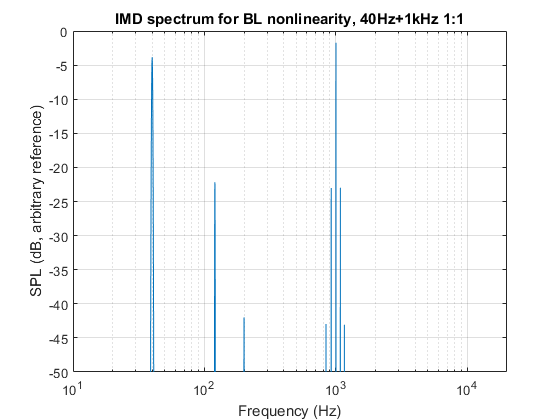
Well that’s something the harmonic distortion plot didn’t tell you: the harmonic distortion may be comparable between both versions but the IMD products around the 1kHz tone are very, very different.
I should add here that the simulation only includes the position dependent component of BL. In practice, BL is usually current dependent as well as our AES paper on force factor modulation shows.
So what conclusions can we draw from that? Quite a few.
- Similar distortion figures can hide very different manifestations.
- Intermodulation measurements are indispensable for evaluating loudspeaker drivers.
- BL as a function of position is a critical performance specification that should never be left out of a data sheet.
- The same goes for BL as a function of current or its equivalent, position dependent self-inductance (see AES paper).
- The stiffness curve of the suspension of a woofer can be designed purely based on practical requirements of robustness and power handling.
- For pure subwoofers, low distortion is optional.
- With their limited control bandwidth (200Hz or so), motional feedback (MFB) systems can only improve distortion in the subwoofer frequency range but are powerless against midrange distortion, including IMD. This explains the limited take-up of this technique.
- Anyone asking “can we ever hear distortion mechanism x when elsewhere in the signal chain distortion from mechanism y is so much greater” should look at what types of distortion either mechanism can and cannot produce. Only then can they know if one distortion mechanism is likely to mask the other.
The science was right: even gross bass distortion is remarkably difficult to hear. The fine print says yes, provided it stays in the bass.
Postscript
Hearing the simulated audio of the BL nonlinearity immediately took me back to the bus station in Kibuye, Rwanda, where they’d mounted a pair of 12” prosumer speakers on poles. Through them Afrobeats music was blasted all day. It was loud and the tweeters were blown. I just had to redo the samples using the track they were actually playing when I passed through. Apologies to the artist, whose music I quite enjoy.